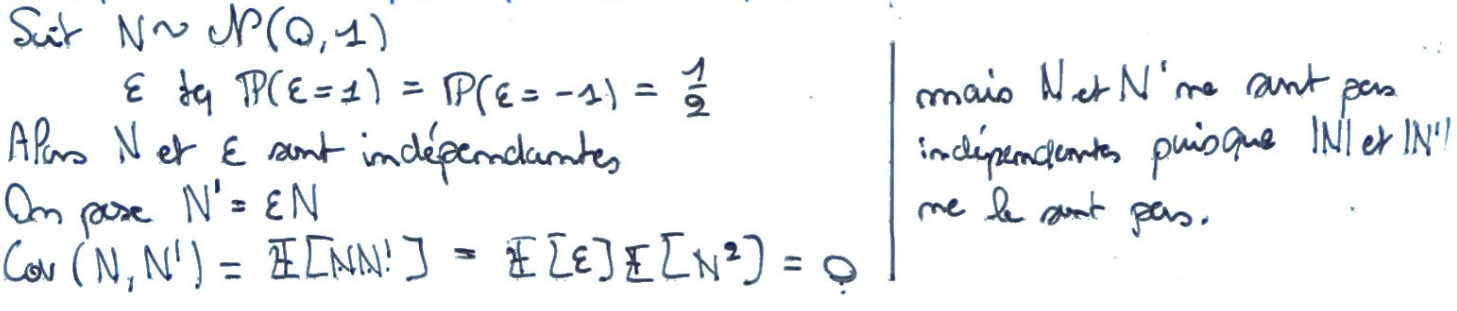Covariance \(\operatorname{cov}(X,Y)\) de \(X\) et \(Y\)
Quantité définie par :$$\begin{align}\operatorname{cov}(X,Y)&={\Bbb E}[(X-{\Bbb E}[X])(Y-{\Bbb E}[Y])]\\ &={\Bbb E}[XY]-{\Bbb E}[X]{\Bbb E}[Y]\end{align}$$

• d'après l'Inégalité de Cauchy-Schwarz, on a $$\lvert \operatorname{cov}(X,Y)\rvert\leqslant\sqrt{V(X)V(Y)}$$
• c'est une Forme bilinéaire sur \(L^2(\Omega,\mathcal A,{\Bbb P})\)
• la covariance est nulle pour deux variables aléatoires indépendantes

Questions de cours

START
Ω Basique (+inversé optionnel)
Recto: Donner un exemple de deux variables aléatoires dont la covariance est nulle, mais qui ne sont pas indépendantes.
Verso:

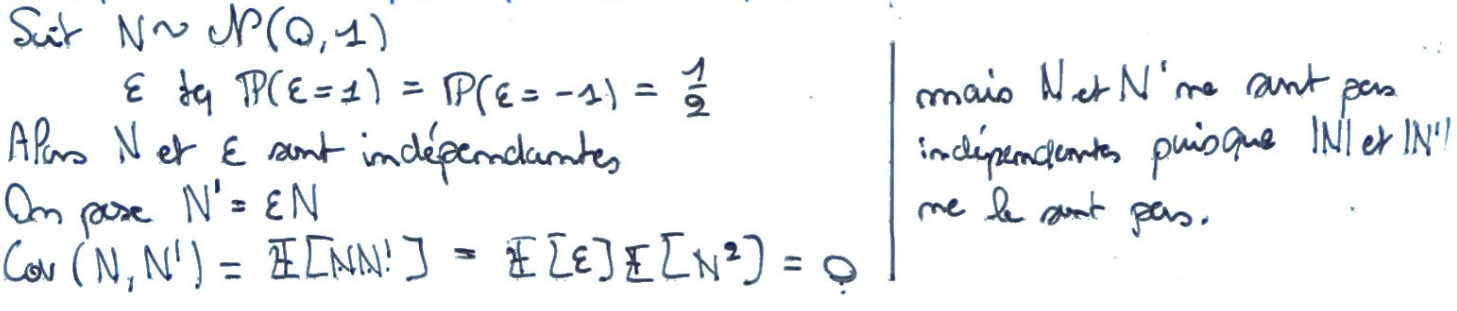
Bonus:
Carte inversée ?:
END